Кеплеровы элементы и другие параметры орбит

Кеплеровы элементы — шесть элементов орбиты, определяющих положение небесного тела в пространстве (рисунок 1):

большая полуось
эксцентриситет
наклонение
аргумент перицентра
долгота восходящего узла
средняя аномалия

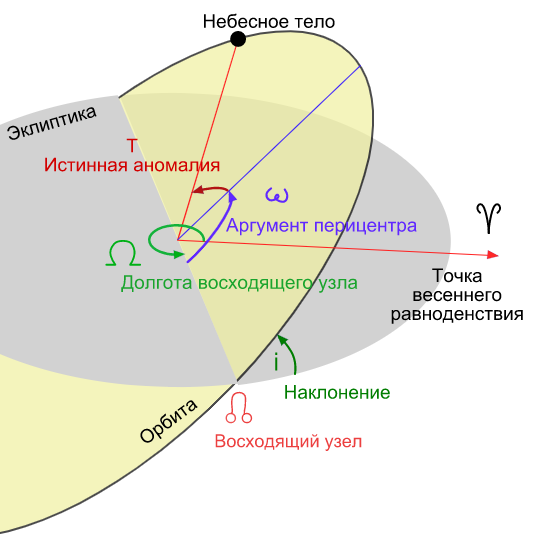
Кеплеровы элементы орбиты

Рисунок 1. Кеплеровы элементы орбиты

Два элемента определяют форму и размер эллиптической орбиты:

Эксцентриситет - форма эллипса, описывающая, насколько он удлинен по сравнению с кругом.
Большая полуось - сумма перицентрического и апоцентрического расстояний, деленная на два. Для классических орбит двух тел большая полуось - это расстояние между центрами тел, а не расстояние между телами от центра масс. Для круговой орбиты большая полуось равна радиусу.

Два элемента определяют ориентацию плоскости орбиты, в которую вложен эллипс:

Наклон - вертикальный наклон эллипса относительно плоскости отсчета, измеренный в восходящем узле (где орбита проходит вверх через плоскость отсчета. Угол наклона измеряется перпендикулярно линии пересечения орбитальной плоскости и базовой плоскости. Любые три точки на эллипсе будут определять плоскость орбиты эллипса. Плоскость и эллипс - это двухмерные объекты, определенные в трехмерном пространстве.
Долгота восходящего узла - горизонтально ориентирует восходящий узел эллипса относительно точки весеннего равноденствия.

Остальные два элемента следующие:

Аргумент перицентра определяет ориентацию эллипса в плоскости орбиты как угол, измеряемый от восходящего узла к перицентру. Это самая нижняя точка орбиты.
Истинная аномалия определяет положение орбитального тела вдоль эллипса в определенное время.

На видео показаны Кеплеровы элементы орбит. Используются следующие английские наименования элементов:

большая полуось - semi-major axis
эксцентриситет - eccentricity
наклонение - inclination
аргумент перицентра - pericenter argument
долгота восходящего узла - longitude of the ascending node
средняя аномалия - medium anomaly

Типы орбит

Следующие типы орбит можно увидеть в режиме дополненной реальности (рисунок 2):

Круговая (общий вид);
Круговая (геосинхронная);
Круговая (геостационарная);
Круговая (полярная);
Эллиптическая (общий вид);
Эллиптическая (молния).

Типы орбит в дополненной реальности

Рисунок 2. Типы орбит в дополненной реальности

Круговая орбита (общий вид) (рисунок 3):

Круговая орбита (общий вид)

Рисунок 3. Круговая орбита (общий вид)

Круговая (геосинхронная) орбита (рисунок 4):

Геосинхронная орбита

Рисунок 4. Круговая (геосинхронная) орбита

Круговая (геостационарная) орбита (рисунок 5):

Геостационарная орбита

Рисунок 5. Круговая (геостационарная) орбита

Круговая (полярная) орбита (рисунок 6):

Полярная орбита

Рисунок 6.Круговая (полярная) орбита

Эллиптическая орбита (общий вид) (рисунок 7):

Эллиптическая орбита

Рисунок 7. Эллиптическая орбита (общий вид)

Эллиптическая орбита ("Молния") (рисунок 8):

Орбита Молния

Рисунок 8. Эллиптическая орбита («Молния»)

Изменение параметров орбит

Установите круговую орбиту (общий вид) и установите все параметры, кроме большой полуоси, в нулевые значения (рисунок 9). Минимальное значение большой полуоси равно 6789 км ,что соответствует высоте орбиты МКС равной 418 км.

Минимальная величина большой полуоси