04 Lesson. Spacecraft stabilization

Spacecraft stabilization mode means maintaining zero angular velocity. Such a mode is necessary, for example, to obtain clear images or transmit them to a ground receiving point when the data transmission time is long and it is not permissible for the spacecraft antenna to deviate from the direction to the ground receiving point. The theory described in this lesson is also suitable for maintaining any required angular velocity, not just zero, for tasks such as tracking a moving object.

How to implement the stabilization mode

The angular velocity of the spacecraft can be changed using flywheels, jet engines, electromagnetic coils, gyrodyne engines. In this example, we will consider controlling the control torque using a flywheel. The operation of this device is based on the law of conservation of angular momentum. For example, when the flywheel engine spins in one direction, the spacecraft, accordingly, begins to rotate in the other direction under the action of the same torque, but directed in the opposite direction in accordance with Newton's third law. If, under the influence of external factors, the spacecraft began to turn in a certain direction, it is enough to increase the speed of rotation of the flywheel in the same direction and the undesirable rotation of the spacecraft will stop, instead of the spacecraft, the rotational moment will "absorb" the flywheel. We will receive information about the angular velocity of the spacecraft using an angular velocity sensor. In this example, we will consider how to calculate the control commands for the flywheel based on the readings of the angular velocity sensor and the data on the speed of rotation of the flywheel so that the spacecraft is stabilized or maintains the required angular velocity.

Theory

Analogies between translational and rotational motion

An analogue of the law of conservation of momentum for rotational motion is the law of conservation of angular momentum or the law of conservation of kinetic momentum:

$$\sum\limits_{i=1}^{n}{{{J}_{i}}\cdot {{\omega }_{i}}}=const$$

In general, the rotational motion of a spacecraft is described by laws similar to those known for translational motion. So, for example, for each parameter in translational motion there is a similar parameter for rotational motion:

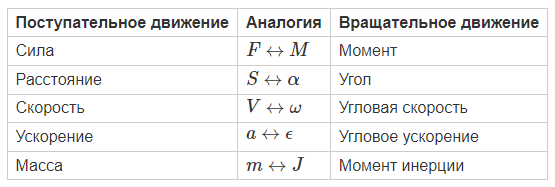
The laws of motion also look similar

![Laws of Motion]

Output of the ratio for the required angular velocity of the flywheel

Let's write down the law of conservation of the kinetic moment of the spacecraft+flywheel system for the moments of time "1" and "2":

$${{J}_{s}}\cdot {{\omega }_{s1}}+{{J}_{m}}\cdot {{\omega }_{m1}}={{J}_{s}}\cdot {{\omega }_{s2}}+{{J}_{m}}\cdot {{\omega }_{m2}}$$

The absolute speed of the flywheel, i.e. the speed of the flywheel in an inertial coordinate system, for example, connected to the Earth, is the sum of the angular velocity of the spacecraft and the angular velocity of the flywheel relative to the spacecraft, i.e. the relative angular velocity of the flywheel:

$${{\omega }_{mi}}={{\omega }_{si}}+{{{\omega }'}_{mi}}$$

Please note that the flywheel can measure its own angular velocity relative to the spacecraft body or relative angular velocity.

Let's express the angular velocity of the flywheel, which must be set

$${{J}_{s}}\cdot {{\omega }_{s1}}+{{J}_{m}}\cdot \left( {{\omega }_{s1}}+{{{{\omega }'}}_{m1}} \right)={{J}_{s}}\cdot {{\omega }_{s2}}+{{J}_{m}}\cdot \left( {{\omega }_{s2}}+{{{{\omega }'}}_{m2}} \right)$$

$$\left( {{J}_{s}}+{{J}_{m}} \right)\left( {{\omega }_{s1}}-{{\omega }_{s2}} \right)=-{{J}_{m}}({{\omega }_{m1}}-{{\omega }_{m2}})$$

$${{\omega }_{m2}}={{\omega }_{m1}}+\frac{{{J}_{s}}+{{J}_{m}}}{{{J}_{m}}}\left( {{\omega }_{s1}}-{{\omega }_{s2}} \right)$$

Let's denote the relation $\frac{{{J}_{s}}+{{J}_{m}}}{{{J}_{m}}}$ as $k_d$.

For the algorithm to work, it is not necessary to know the exact value of $\frac{{{J}_{s}}+{{J}_{m}}}{{{J}_{m}}}$, because the flywheel cannot instantly set the required angular velocity. Measurement noises also interfere with the control process: the angular velocity of the spacecraft measured using an angular velocity sensor is not accurate, because there is always a constant error and measurement noise in the measurements. It should be noted that angular velocity measurements and the issuance of commands to the flywheel occur with a certain minimum step in time. All these limitations lead to the fact that $k_d$ is selected experimentally or detailed computer models are built that take into account all the above limitations. In our case, the coefficient $k_d$ will be selected experimentally.

${{\omega }_{m2}}={{\omega }_{m1}}+{{k}_{d}}\left( {{\omega }_{s1}}-{{\omega }_{s2}} \right)$

Angular velocity $\omega_{s2}$ at time "2" is the target angular velocity, let's denote it $\omega_{s\_goal}$. Thus, if it is necessary that the spacecraft maintain the angular velocity of $\omega_{s\_goal}$, then knowing the current angular velocity of the spacecraft and the current angular velocity of the flywheel, it is possible to calculate the desired flywheel speed to maintain the "rotation at constant speed" mode:

${{\omega }_{m2}}={{\omega }_{m1}}+{{k}_{d}}\left( {{\omega }_{s1}}-{{\omega }_{{s\_goal}}} \right)$

Using the constant speed rotation mode, you can make the spacecraft turn at any angle if you rotate the spacecraft at a constant speed for a certain time. Then the time it takes to rotate the spacecraft at a constant speed $\omega_{s\_goal}$ to turn around at the required angle $\alpha$ is determined by dividing these values:

$t=\frac{\alpha}{\omega_{{s\_goal}}}$

If it is required that the spacecraft be stabilized, then $\omega_{s\_goal}=0$ and the expression takes on a simpler form:

${{\omega }_{m2}}={{\omega }_{m1}}+{{k}_{d}}\cdot {{\omega }_{s1}}$

Example of the full spacecraft stabilization program code in C:

     #include <stdio.h>
     #include <stdint.h>
     #include "libschsat.h"
         void control(void){
 
     float gyro_x = 0, gyro_y = 0, gyro_z = 0;
     uint16_t tmp=0;
 
     gyro_set_offset(0, 4.6, -2.0, 0.7); // these values will be different
 
     float gyro_set = 0.0;
     float p_koeff = 1.0;
     float motor_set = 0;
 
     for (int i = 0; i < 300; i++)
     {
        gyro_request_raw(tmp, &gyro_x, &gyro_y, &gyro_z); // gyro returns degrees per sec!
        printf("Gyro: %6f\t  Wheel_rpm: %6f\n", gyro_z, motor_set);
 
        // simple P-controller
        float delta_gyro = (gyro_set - gyro_z );
        if (fabs(delta_gyro) > 0.001)
        {
            motor_set += delta_gyro * p_koeff;
        }
        motor_set_speed(0, motor_set);
        mSleep(100);
     }
     motor_set_speed(0, 0);
     // set telemetry period 1 sec
     puts("Job done!");
    }

![Example of data obtained during stabilization]

Picture 1. An example of the data obtained during the stabilization process

In this program, a proportional control law is used to stabilize the spacecraft. The principle of operation is that the regulator generates a control effect on the object in proportion to the magnitude of the error (the greater the delta_gyro error, the greater the change in the speed of rotation of the flywheel) (Picture 2):

![Proportional controller]

Picture 2. Proportional control

A task for independent work

1) Change the program so that the spacecraft rotates at a constant speed.

2) Change the program so that the spacecraft works according to the following cyclogram:

• stabilization within 10 seconds,
• 180 degree turn in 30 seconds,
• stabilization again within 10 seconds.