04 Урок. Стабилизация спутника

Режим стабилизации спутника означает поддержание нулевой угловой скорости. Такой режим необходим, например, для получения четких снимков или их передачи на наземный пункт приема, когда время передачи данных продолжительно и не допустимо отклонение антенны спутника от направления на наземный пункт приема данных. Также описанная в этом уроке теория подходит для режима поддержания любой требуемой угловой скорости, а не только нулевой, для таких задач как отслеживание подвижного объекта.

Как реализовать режим стабилизации

Изменять угловую скорость спутника можно с помощью маховиков, реактивных двигателей, электромагнитных катушек, двигателей - гиродинов. В этом примере мы рассмотрим управление управляющим моментом с помощью маховика. Действие этого устройства основано на законе сохранения момента импульса. Например, когда двигатель-маховик раскручивается в одну сторону, то космический аппарат (КА), соответственно, начинает вращаться в другую сторону под действием такого же раскручивающего момента, но направленного в противоположную сторону в соответствии с третьим законом Ньютона. Если под влиянием внешних факторов КА начал разворачиваться в определённом направлении, достаточно увеличить скорость вращения маховика в ту же сторону и нежелательный поворот КА прекратится, вместо спутника вращательный момент «вберет» в себя маховик. Получать информацию об угловой скорости спутника будем с помощью датчика угловой скорости. В этом примере мы рассмотрим как по показаниям датчика угловой скорости и данных о частоте вращения маховика рассчитать управляющие команды для маховика, чтобы спутник был стабилизирован или поддерживал требуемую угловую скорость.

Теория

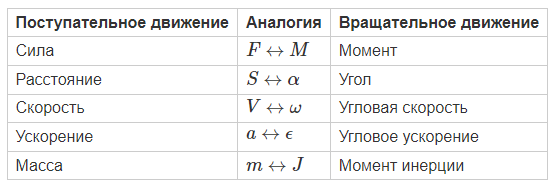
Аналогии между поступательным и вращательным движением

Аналогом закона сохранения импульса для вращательного движения является закон сохранения момента импульса или закон сохранения кинетического момента:

$$\sum\limits_{i=1}^{n}{{{J}_{i}}\cdot {{\omega }_{i}}}=const$$

Вообще вращательное движение спутника описывается законами схожими с законами известными для поступательного движения. Так, например, для каждого параметра в поступательном движении есть аналогичный параметр для вращательного движения:

Законы движения также выглядят аналогичным образом

Вывод соотношения для требуемой угловой скорости маховика

Запишем закон сохранения кинетического момента системы спутник+маховик для моментов времени «1» и «2»:

$${{J}_{s}}\cdot {{\omega }_{s1}}+{{J}_{m}}\cdot {{\omega }_{m1}}={{J}_{s}}\cdot {{\omega }_{s2}}+{{J}_{m}}\cdot {{\omega }_{m2}}$$

Абсолютная скорость маховика, т.е. скорость маховика в инерциальной системе координат, например, связанной с Землей, представляет собой сумму угловой скорости спутника и угловой скорости маховика относительно спутника, т.е. относительной угловой скорости маховика:

$${{\omega }_{mi}}={{\omega }_{si}}+{{{\omega }'}_{mi}}$$

Обращаем внимание, что маховик может измерять собственную угловую скорость относительно корпуса спутника или относительную угловую скорость.

Выразим угловую скорость маховика, которую необходимую задать

$${{J}_{s}}\cdot {{\omega }_{s1}}+{{J}_{m}}\cdot \left( {{\omega }_{s1}}+{{{{\omega }'}}_{m1}} \right)={{J}_{s}}\cdot {{\omega }_{s2}}+{{J}_{m}}\cdot \left( {{\omega }_{s2}}+{{{{\omega }'}}_{m2}} \right)$$

$$\left( {{J}_{s}}+{{J}_{m}} \right)\left( {{\omega }_{s1}}-{{\omega }_{s2}} \right)=-{{J}_{m}}({{\omega }_{m1}}-{{\omega }_{m2}})$$

$${{\omega }_{m2}}={{\omega }_{m1}}+\frac{{{J}_{s}}+{{J}_{m}}}{{{J}_{m}}}\left( {{\omega }_{s1}}-{{\omega }_{s2}} \right)$$

Обозначим отношение $\frac{{{J}_{s}}+{{J}_{m}}}{{{J}_{m}}}$ как $k_d$.

Для работы алгоритма необязательно знать точное значение $\frac{{{J}_{s}}+{{J}_{m}}}{{{J}_{m}}}$, т.к. маховик не может мгновенно установить требуемую угловую скорость. Также в процесс управления вмешиваются шумы измерений: угловая скорость спутника измеренная с помощью датчика угловой скорости не является точной, т.к. в измерениях всегда есть постоянная ошибка и шум измерений. Следует учесть, что измерения угловой скорости и выдача команд маховику происходят с некоторым минимальным шагом во времени. Все эти ограничения приводят к тому, что $k_d$ подбирается экспериментальным путем или строятся подробные компьютерные модели, которые учитывают все вышеописанные ограничения. В нашем случае коэффициент $k_d$ будем подбирать экспериментально.

${{\omega }_{m2}}={{\omega }_{m1}}+{{k}_{d}}\left( {{\omega }_{s1}}-{{\omega }_{s2}} \right)$

Угловая скорость $\omega_{s2}$ в момент времени «2» является целевой угловой скоростью, обозначим ее $\omega_{s\_goal}$. Таким образом, если необходимо что спутник поддерживал угловую скорость $\omega_{s\_goal}$, то зная текущую угловую скорость спутника и текущую угловую скорость маховика возможно рассчитать желаемую скорость маховика для поддержания режима «вращения с постоянной скоростью»:

${{\omega }_{m2}}={{\omega }_{m1}}+{{k}_{d}}\left( {{\omega }_{s1}}-{{\omega }_{{s\_goal}}} \right)$

Используя режим вращения с постоянной скоростью можно заставить спутник повернуться на любой угол если вращать спутник с постоянной скоростью определенное время. Тогда время, которое необходимо вращать спутник с постоянной скоростью $\omega_{s\_goal}$, чтобы развернуться на требуемый угол $\alpha$ определяется делением этих величин:

$t=\frac{\alpha}{\omega_{{s\_goal}}}$

Если требуется чтобы спутник был застабилизирован, то $\omega_{s\_goal}=0$ и выражение приобретает более простой вид:

${{\omega }_{m2}}={{\omega }_{m1}}+{{k}_{d}}\cdot {{\omega }_{s1}}$

Задание для самостоятельной работы

1) Измените программу так, чтобы спутник вращался с постоянной скоростью.

2) Измените программу так, чтобы спутник работал по следующей циклограмме:

• стабилизация в течении 10 секунд,
• разворот на 180 градусов за время 30 секунд,
• снова стабилизация в течении 10 секунд.