Earth Remote Sensing Mission
Run the FCC software (Picture 1)
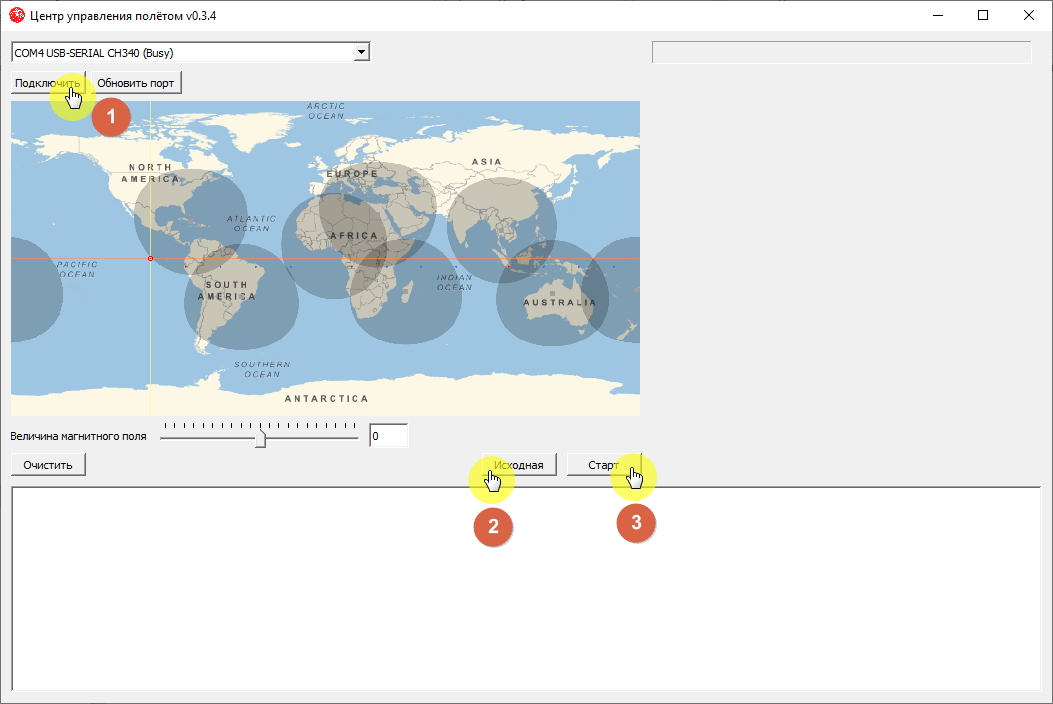
Picture 1. FCC software
Click the Connect button to connect the FCC software to the globe via USB;
Press the Home button to set the globe to its original position;
Press the Start button immediately before launching the program in Orbicraft.
Determine the position of the OrbiCraft relative to the receiving station after setting the globe to its original position.
This is necessary to determine the delay time that must be specified in the Orbicraft program.
For example, if the photographing point is located on the meridian 80, and the orbicraft is suspended opposite the meridian 40, then the distance between them is 40 degrees. The rotation speed of the globe is one revolution in 5 minutes (360 degrees in 600 seconds, or 0.6 degrees per second). Therefore, the globe will rotate at an angle of 40 degrees in 24 seconds. Use this value in the Orbicraft program.
Upload the following code to Orbicraft Python code to stabilize Orbicraft ("satellite") and get photos of the globe ("Earth"):
import math
time_step = 0.1 # Time step of the algorithm, with
omega_goal = 0.0 # Target angular velocity of the satellite, deg/s. For stabilization mode, it is 0.0.
mtr_max_speed = 3500 # Maximum permissible flywheel speed, rpm
mtr_num = 1 # Flywheel number
hyr_num = 1 # DUS number
mag_num = 1 # Magnetometer
number alpha_goal = 0 # Target rotation angle
errora = 0 # Angle error
Pa = 0 # Impact of the proportional link
Da = 0 # The effect of the differential link
Ia = 0 # Impact of the integral link
Kpa = 20 # Proportional coefficient of error in angle
Kda = 0.1 # Differential coefficient
Kia = 1 # Integral coefficient
lastErrora = 0 # Past angle error
Integratora = 0 # Integral (sum of all angle errors)
PID_alpha = 0 # Magnitude of the control action
Integrator_maxa = 10 # Limitation of the maximum value of the integrator
Integrator_mina = -10 # Limitation of the minimum value of the integrator
error = 0 # Angular velocity error
P = 0 # Impact of the proportional link
D = 0 # The effect of the differential link
I = 0 # Impact of the integral link
Kp = 20 # Proportional coefficient
Kd = 0.1 # Differential coefficient
Ki = 1 # Integral coefficient
lastError = 0 # Past angular velocity error
Integrator = 0 # Integral (sum of all angular velocity errors)
PID_omega = 0 # The magnitude of the control action
Integrator_max = 10 # Limitation of the maximum value of the integrator
Integrator_min = -10 # Limitation of the minimum value of the integrator
# The mag_calibrated function corrects the magnetometer readings taking into account the calibration coefficients
def mag_calibrated(magx,magy,magz): # you will have different coefficients after calibrating the magnetometer
magx_cal = 1.668867*(magx + -38.326818) + -0.007649*(magy + 20.442007) + 0.113348*(magz + -69.659602)
magy_cal = -0.007649*(magx + -38.326818) + 1.749597*(magy + 20.442007) + 0.130999*(magz + -69.659602)
magz_cal = 0.113348*(magx + -38.326818) + 0.130999*(magy + 20.442007) + 1.577785*(magz + -69.659602)
return magx_cal, magy_cal, magz_cal
# Functions for determining the new flywheel speed.
# The new flywheel speed consists of
# the current flywheel speed mtr_speed and two speed increments PID_omega and PID_alpha
# PID_omega - speed increment to reduce angular velocity deviation
# PID_alpha - speed increment to reduce angle deviation
# The speed increments are obtained by adding three coefficients:
# P is the proportional coefficient of the regulator
# I - integral coefficient of the regulator
# D is the differential coefficient of the regulator
# Integrator accumulates the total error
# The saturator limits the maximum value of the total error
# mtr_speed - current angular velocity of the flywheel, rpm
# omega - the current angular velocity of the satellite, deg/s
# omega_goal - target angular velocity of the satellite, deg/s
# mtr_new_speed - required angular velocity of the flywheel, rpm
# all variables of the angle deviation regulator have the letter "a" at the end of the name
def motor_new_speed_PD(mtr_speed, alpha, alpha_goal, omega, omega_goal):
global Integrator
global lastError
global Integratora
global lastErrora
error = omega - omega_goal # Error calculation
P = Kp * error # Calculation of the impact of the proportional link
D = Kd * (error - lastError) / time_step # Calculating the impact of the differential link
lastError = error # Remembering the error
Integrator = Integrator + error * time_step # Accumulating the total error
if Integrator > Integrator_max: # Saturation (Limiting the maximum value of the accumulated error)
Integrator = Integrator_max
elif Integrator < Integrator_min:
Integrator = Integrator_min
I = Integrator * Ki # Calculation of the impact of the integral link
PID_omega = P + I + D # Calculation of the total control effect
errora = alpha - alpha_goal # Error calculation
Pa = Kpa * errora # Calculation of the impact of the proportional link
Da = Kda * (errora - lastErrora) / time_step # Calculating the impact of the differential link
lastErrora = errora # Remembering the error
Integratora = Integratora + errora * time_step # Accumulating the total error
if Integratora > Integrator_maxa: # Saturation (Limiting the maximum value of the accumulated error)
Integratora = Integrator_maxa
elif Integratora < Integrator_mina:
Integratora = Integrator_mina
Ia = Integratora * Kia # Calculation of the impact of the integral link
PID_alpha = Pa + Ia + Da # Calculation of the total control effect
mtr_new_speed = int(mtr_speed + PID_omega + PID_alpha)
if mtr_new_speed > mtr_max_speed:
mtr_new_speed = mtr_max_speed
elif mtr_new_speed < -mtr_max_speed:
mtr_new_speed = -mtr_max_speed
print "P= ", P, "\t\tI= ", I, "\t\tD= ", D, "\t\tPID_omega= ", PID_omega, "\tmtr_new_speed= ", mtr_new_speed
print "Pa= ", Pa, "\tIa= ", Ia, "\t\tDa= ", Da, "\tPID_alpha=", PID_alpha
return mtr_new_speed
# The function includes all devices,
# which will be used in the main program.
def initialize_all(): # Initialization function for all systems
print "Enable motor No.", mtr_num
motor_turn_on(mtr_num) # Turn
on the sleep motor(1)
print "Enable angular velocity sensor №", hyr_num
hyro_turn_on(hyr_num) # Turn on the DUS
sleep(1)
print "Enable magnetometer", mag_num
magnetometer_turn_on(mag_num) # Turn
on the sleep magnetometer(1)
camera_turn_on() #Turn on the camera and transmitter and wait for them to load
transmitter_turn_on(1)
sleep(1)
def switch_off_all(): # Shutdown function for all systems
print "Finishing..."
print "Disable angular velocity sensor №", hyr_num
hyro_turn_off(hyr_num) # Turn off the DUS
print "Disable magnetometer", mag_num
magnetometer_turn_off(mag_num)
motor_set_speed(mtr_num, 0) # Turn off the magnetometer
sleep (1)
motor_turn_off(mtr_num) # Turn off the motor
camera_turn_off() #Turn on the camera and transmitter and wait for them to load
transmitter_turn_off(1)
sleep(1)
print "Finish program"
def angle_transformation(alpha, alpha_goal):
if alpha<=(alpha_goal - 180):
alpha = alpha + 360
elif alpha>(alpha_goal +180):
alpha = alpha - 360
return alpha
# The main function of the program in which the rest of the functions are called.
def control():
initialize_all()
mtr_state = 0 # Initialize the flywheel status
hyro_state = 0 # Initialize the status of the DUS
mag_state = 0 # Initialize the magnetometer status
alpha_goal = -120 # Target angle
omega_goal = 0 # Target angular velocity
mag_alpha = 0
frame = 0
err = 0
omega = 0
# the globe rotates 360 degrees in 600 seconds. Angular velocity 0.6 degrees per second
# using the meridians, we determine the angle from orbicraft to the receiving point (I have 40 degrees)
# calculate the delay of 40 * 0.6 = 24 seconds. And subtract 5 seconds for the rotation of the satellite 24-5 = 19
sleep(22) # manually select the time (or calculate it using the formula depending on the angular velocity of the globe)
for i in range(60):
# Survey of magnetometer, angular velocity sensor and flywheel
mag_state, magx_raw, magy_raw, magz_raw = magnetometer_request_raw(mag_num)
hyro_state, gx_raw, gy_raw, gz_raw = hyro_request_raw(hyr_num)
mtr_state, mtr_speed = motor_request_speed(mtr_num)
if not mag_state: # if the magnetometer returned an error code of 0, i.e. there is no error
magx_cal, magy_cal, magz_cal = mag_calibrated(magx_raw,magy_raw,magz_raw)
mag_alpha = math.atan2(magy_cal, magx_cal)/math.pi*180
mag_alpha = angle_transformation(mag_alpha, alpha_goal)
print "mag_alpha atan2= ", mag_alpha
elif mag_state == 1:
print "Fail because of access error, check the connection"
elif mag_state == 2:
print "Fail because of interface error, check your code"
# Processing of the angular velocity sensor readings,
# calculation of the angular velocity of the satellite according to the readings of the DUS.
# If the DUS error code is 0, i.e. there is no error
if not hyro_state:
gz_degs = gz_raw * 0.00875
# if the DUS is set with the z axis up, then the angular velocity
The satellite's # coincides with the readings of the DUS along the z axis, otherwise
# the sign must be changed: omega = - gz_degs
omega = gz_degs #if the DUS is set with the z axis up
elif hyro_state == 1:
print "Fail because of access error, check the connection"
elif hyro_state == 2:
print "Fail because of interface error, check your code"
#Processing the flywheel readings and setting the required angular velocity.
if not mtr_state: # if the error code is 0, i.e. there is no error
print "Motor_speed: ", mtr_speed, "\t\ti= ", i,
# setting the new flywheel speed
mtr_new_speed = motor_new_speed_PD(mtr_speed, mag_alpha, alpha_goal, omega, omega_goal)
motor_set_speed(mtr_num, mtr_new_speed)
if i == 50: # Taking a picture
err_camera = camera_take_photo(frame)
if err == 1:
print 'Camera access error, check the connection', frame
elif err == 2:
print 'Camera interface errorr, check the code', frame
#Passing the snapshot
err_transmitter = transmitter_transmit_photo(1, frame)
if err_transmitter == 1:
print 'Transmition failed'
sleep(time_step)
switch_off_all()
Code in the Python language for stabilizing Orbicraft ("satellite"), taking photos of the globe ("Earth") and transmitting telemetry over UHF:
import math
time_step = 0.1 # The time step of the algorithm, with
omega_goal = 0.0 # Target angular velocity of the satellite, deg/s. For stabilization mode, it is 0.0.
mtr_max_speed = 3500 # Maximum permissible flywheel speed, rpm
mtr_num = 1 # Flywheel number
hyr_num = 1 # DUS number
mag_num = 1 # Magnetometer
number alpha_goal = 0 # Target rotation angle
errora = 0 # Angle error
Pa = 0 # Impact of the proportional link
Da = 0 # The effect of the differential link
Ia = 0 # Impact of the integral link
Kpa = 20 # Proportional angle error coefficient
Kda = 0.1 # Differential coefficient
Kia = 1 # Integral coefficient
lastErrora = 0 # Past angle error
Integratora = 0 # Integral (sum of all angle errors)
PID_alpha = 0 # Magnitude of the control action
Integrator_maxa = 10 # Limitation of the maximum value of the integrator
Integrator_mina = -10 # Limitation of the minimum value of the integrator
error = 0 # Angular velocity error
P = 0 # Impact of the proportional link
D = 0 # The effect of the differential link
I = 0 # Impact of the integral link
Kp = 20 # Proportional coefficient
Kd = 0.1 # Differential coefficient
Ki = 1 # Integral coefficient
lastError = 0 # Past angular velocity error
Integrator = 0 # Integral (sum of all angular velocity errors)
PID_omega = 0 # The magnitude of the control action
Integrator_max = 10 # Limitation of the maximum value of the integrator
Integrator_min = -10 # Limitation of the minimum value of the integrator
# The mag_calibrated function corrects the magnetometer readings taking into account the calibration coefficients
def mag_calibrated(magx,magy,magz): # you will have different coefficients after calibrating the magnetometer
magx_cal = 1.668867*(magx + -38.326818) + -0.007649*(magy + 20.442007) + 0.113348*(magz + -69.659602)
magy_cal = -0.007649*(magx + -38.326818) + 1.749597*(magy + 20.442007) + 0.130999*(magz + -69.659602)
magz_cal = 0.113348*(magx + -38.326818) + 0.130999*(magy + 20.442007) + 1.577785*(magz + -69.659602)
return magx_cal, magy_cal, magz_cal
# Functions for determining the new flywheel speed.
# The new flywheel speed consists of
# the current flywheel speed mtr_speed and two speed increments PID_omega and PID_alpha
# PID_omega - speed increment to reduce angular velocity deviation
# PID_alpha - speed increment to reduce angle deviation
# The speed increments are obtained by adding three coefficients:
# P is the proportional coefficient of the regulator
# I - integral coefficient of the regulator
# D is the differential coefficient of the regulator
# Integrator accumulates the total error
# The saturator limits the maximum value of the total error
# mtr_speed - current angular velocity of the flywheel, rpm
# omega - the current angular velocity of the satellite, deg/s
# omega_goal - target angular velocity of the satellite, deg/s
# mtr_new_speed - required angular velocity of the flywheel, rpm
# all variables of the angle deviation regulator have the letter "a" at the end of the name
def motor_new_speed_PD(mtr_speed, alpha, alpha_goal, omega, omega_goal):
global Integrator
global lastError
global Integratora
global lastErrora
error = omega - omega_goal # Error calculation
P = Kp * error # Calculation of the impact of the proportional link
D = Kd * (error - lastError) / time_step # Calculating the impact of the differential link
lastError = error # Remembering the error
Integrator = Integrator + error * time_step # Accumulating the total error
if Integrator > Integrator_max: # Saturation (Limiting the maximum value of the accumulated error)
Integrator = Integrator_max
elif Integrator < Integrator_min:
Integrator = Integrator_min
I = Integrator * Ki # Calculation of the impact of the integral link
PID_omega = P + I + D # Calculation of the total control effect
errora = alpha - alpha_goal # Error calculation
Pa = Kpa * errora # Calculation of the impact of the proportional link
Da = Kda * (errora - lastErrora) / time_step # Calculating the impact of the differential link
lastErrora = errora # Remembering the error
Integratora = Integratora + errora * time_step # Accumulating the total error
if Integratora > Integrator_maxa: # Saturation (We limit the maximum value of the accumulated error)
Integratora = Integrator_maxa
elif Integratora < Integrator_mina:
Integratora = Integrator_mina
Ia = Integratora * Kia # Calculation of the impact of the integral link
PID_alpha = Pa + Ia + Da # Calculation of the total control effect
mtr_new_speed = int(mtr_speed + PID_omega + PID_alpha)
if mtr_new_speed > mtr_max_speed:
mtr_new_speed = mtr_max_speed
elif mtr_new_speed < -mtr_max_speed:
mtr_new_speed = -mtr_max_speed
print "P= ", P, "\t\tI= ", I, "\t\tD= ", D, "\t\tPID_omega= ", PID_omega, "\tmtr_new_speed= ", mtr_new_speed
print "Pa= ", Pa, "\tIa= ", Ia, "\t\tDa= ", Da, "\tPID_alpha=", PID_alpha
return mtr_new_speed
# The function includes all devices,
# which will be used in the main program.
def initialize_all(): # Initialization function for all systems
print "Enable motor No.", mtr_num
motor_turn_on(mtr_num) # Turn
on the sleep motor(1)
print "Enable angular velocity sensor"
hyro_turn_on(hyr_num) # Turn on the DUS
sleep(1)
print "Enable magnetometer", mag_num
magnetometer_turn_on(mag_num) # Turn
on the sleep magnetometer(1)
camera_turn_on() # Turn on the camera
sleep(1)
transmitter_turn_on(1)
sleep(1)
transceiver_turn_on(2) # On-board UHF has the number 2
sleep(1)
def switch_off_all(): # All systems shutdown function
print "Finishing..."
print "Disable angular velocity sensor"
hero_turn_off(her_num) # Turn off the DUS
print "Disable magnetometer", mag_num
magnetometer_turn_off(mag_num)
motor_set_speed(mtr_num, 0) # Turn off the magnetometer
sleep (1)
motor_turn_off(mtr_num) # Turn off the motor
sleep (1)
camera_turn_off() # Turn off the camera
sleep(1)
transmitter_turn_off(1)
sleep(1)
transceiver_turn_off(2)
sleep(1)
print "Finish program"
def angle_transformation(alpha, alpha_goal):
if alpha<=(alpha_goal - 180):
alpha = alpha + 360
elif alpha>(alpha_goal +180):
alpha = alpha - 360
return alpha
def uhf(msg):
error = transceiver_send(2, 1, msg)
if not error:
print "data has been transmitted"
elif error == 1: # if the sensor returned an error message of 1
print "Fail because of access error, check the connection"
elif error == 2: # if the sensor returned an error message 2
print "Fail because of interface error, check your code"
# The main function of the program in which the other functions are called.
def control():
initialize_all()
mtr_state = 0 # Initialize the reaction wheel status
hyro_state = 0 # Initialize the status of the AVS
mag_state = 0 # Initialize the magnetometer status
alpha_goal = -120 # Target angle
omega_goal = 0 # Target angular velocity
mag_alpha = 0
frame = 0
err = 0
omega = 0
bus_setup();
#the globe rotates 360 degrees in 600 seconds. Angular velocity 0.6 degrees per second
# using meridians, we determine the angle from orbicraft to the receiving point (I have 40 degrees)
# calculate the delay 40 * 0.6 = 24 seconds. And subtract 5 seconds for the rotation of the satellite 24-5 = 19
sleep(22) # we manually select the time (or calculate it using the formula depending on the angular velocity of the globe)
message = "Start mission\n"
uhf(message)
for i in range(60):
# Survey of magnetometer, angular velocity sensor and reaction wheel
mag_state, magx_raw, magy_raw, magz_raw = magnetometer_request_raw(mag_num)
hyro_state, gx_raw, gy_raw, gz_raw = hyro_request_raw(hyr_num)
mtr_state, mtr_speed = motor_request_speed(mtr_num)
if not mag_state: # if the magnetometer returned an error code of 0, i.e. there is no error
magx_cal, magy_cal, magz_cal = mag_calibrated(magx_raw,magy_raw,magz_raw)
mag_alpha = math.atan2(magy_cal, magx_cal)/math.pi*180
mag_alpha = angle_transformation(mag_alpha, alpha_goal)
print "mag_alpha atan2= ", mag_alpha
elif mag_state == 1:
print "Fail because of access error, check the connection"
elif mag_state == 2:
print "Fail because of interface error, check your code"
# Processing of the angular velocity sensor readings,
# calculation of the angular velocity of the satellite according to the readings of the DUS.
# If the DUS error code is 0, i.e. there is no error
if not hyro_state:
gz_degs = gz_raw * 0.00875
# if the DUS is set with the z axis up, then the angular velocity
# The satellite's coincides with the readings of the DUS along the z axis, otherwise
# the sign must be changed: omega = - gz_degs
omega = gz_degs #if the DUS is set with the z axis up
elif hyro_state == 1:
print "Fail because of access error, check the connection"
elif hyro_state == 2:
print "Fail because of interface error, check your code"
#Processing the flywheel readings and setting the required angular velocity.
if not mtr_state: # если код ошибки 0, т.е. ошибки нет
print "Motor_speed: ", mtr_speed, "\t\ti= ", i,
# setting the new motor speed
mtr_new_speed = motor_new_speed_PD(mtr_speed, mag_alpha, alpha_goal, omega, omega_goal)
motor_set_speed(mtr_num, mtr_new_speed)
if i == 50: # Take a photo
err_camera = camera_take_photo(frame)
if err == 1:
print 'Camera access error, check the connection', frame
elif err == 2:
print 'Camera interface errorr, check the code', frame
#Transmit the photo
err_transmitter = transmitter_transmit_photo(1, frame)
if err_transmitter == 1:
print 'Transmition failed'
message = "Photo\n"
uhf(message)
message = "Omega = " +str(omega) + '\n'
uhf(message)
message = "Finish mission\n"
uhf(message)
sleep(time_step)
switch_off_all()