08 Урок. Работа с ПИД-регулятором

ПИД-регулятор (Пропорционально-Интегрально-Дифференциальный регулятор) – это алгоритм управления, который используется для регулирования инерциальных процессов, например: изменения температуры (пример: поддерживание температуры холодильника или паяльника), скорости (самолет с автопилотом), частоты (частота оборотов мотора станка) и т. д.

В алгоритме используются три компонента:

• P – пропорциональный;
• I – интегральный;
• D – дифференциальный.

info

Если какие-то из составляющих не используются, то регулятор называют пропорционально-интегрирующим, пропорционально-дифференцирующим, пропорциональным и т. д.

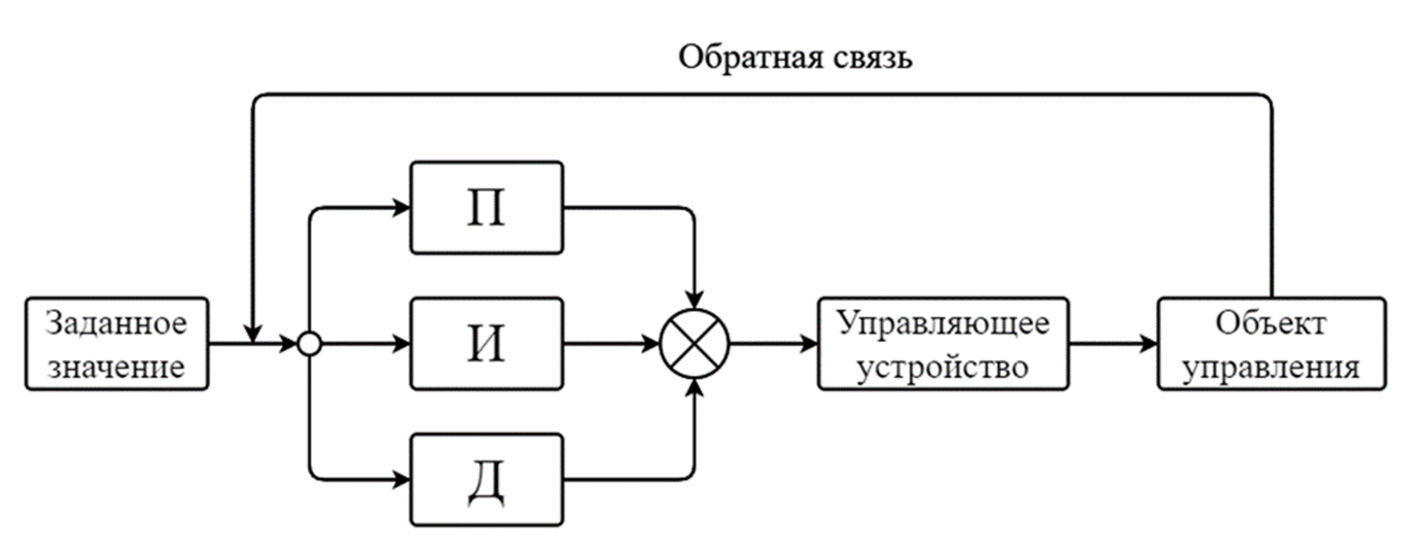
Рисунок 1. ПИД-регулятор

ПИД-регулятор формирует управляющий сигнал, который является суммой пропорциональной, интегрирующей и дифференцирующей составляющих, каждая из которых получается посредством математических преобразований значений о текущем положении системы. В программе это будет выглядеть так:

1. Установка целевого значения;
2. Получение значения с датчика (температуры, угловой скорости, положения в пространстве);
3. Выполнение вычислений и получение управляющего сигнала;
4. Воздействие на систему с учётом управляющего сигнала (изменение мощности нагревателя, скорости вращения маховика).

Рассмотрим подробнее каждый из компонентов с примером реализации. Для начала нам нужно задать значения коэффициентов и целевого состояния системы. Значения коэффициентов как правило подбираются заранее и не изменяются в ходе работы программы.

Пропорциональный компонент рассчитывается на основе разницы между желаемым значением и текущим значением измеряемой величины. Данная разность называется ошибкой регулирования, и характеризует насколько система близка к целевому значению.

P= setpoint - input,

где setpoint – установка (заданное значение);

input – вход (значение с датчика).

Чем больше ошибка, тем больше будет управляющий сигнал и тем быстрее система будет приводить управляемую величину к заданному значению. Чем меньше ошибка регулирования, тем меньше пропорциональный компонент, соответственно пропорциональная составляющая не всегда может исправить ошибку.

Интегральный компонент просто суммирует в саму себя ту же самую ошибку, разность текущего и заданного значения, умноженную на период дискретизации системы, то есть на время, прошедшее с предыдущего расчёта dt – фактически берёт интеграл от ошибки по времени.

В интегральной составляющей буквально копится ошибка, что позволяет регулятору с течением времени полностью её устранить, то есть привести систему ровно к заданному значению с максимальной точностью. Эффект будет не мгновенен — для накопления ошибки необходимо несколько итераций алгоритма.

I=I + (setpoint - input) * dt

где setpoint – установка (заданное значение);

input – вход (значение с датчика);

dt – период вычисления и регулирования.

Однако, если коэффициент интегральной составляющей слишком большой, то это может привести к неустойчивости системы и перерегулированию. Поэтому необходимо находить оптимальное значение коэффициента интегральной составляющей, чтобы достичь наилучшего результата управления процессом.

Дифференциальный компонент учитывает изменение ошибки регулирования со временем и корректирует выходной сигнал, чтобы предотвратить перерегулирование.

Компонент представляет собой разность текущей и предыдущей ошибки, поделенную на время между измерениями, то есть на ту же dt, которая общий период регулятора. Иными словами – это производная от ошибки по времени.

err = setpoint - input
D = (err - prevErr) / dt
prevErr = err

где setpoint – установка (заданное значение);

input – вход (значение с датчика);

err – ошибка регулирования;

dt – период вычисления и регулирования.

D составляющая исправляет возможные будущие ошибки, анализируя скорость.

Выходная величина регулятора (управляющий сигнал) вычисляется по формуле: out = PkP + IkI + D*kD kP, kI и kD это и есть те самые коэффициенты, которые нужно настроить для работы ПИД-регулятора. Значения тут могут быть самые разные, от 0.001 то десятков и тысяч, это зависит от конкретной системы.

Для работы с ПИД-регулятором нужно корректно прописать начальные условия, например:

    float P = 1e-4; 
    float D = 0.01;
    float I = 0.0001; // начальные коэф-ты пид-регулятора
    float I_sum = 0.0004; //ошибку надо ограничивать для снижения колебания системы
    float pid_border = 0.2; //Н*м это макс момент, который подается на маховик для ограничения
    float P_out = 0, D_out = 0, I_out = 0; //коэффициенты, использующиеся для вычисления PD_OUT
    float PD_OUT = 0; //значение, которое мы в итоге передадим на маховик (момент маховика)
    float error = 0.0; //начальная ошибка
    float previous_error = 0.0; //начальное значение предыдущей ошибки
    float intgral_error = 0.0; //начальное значение ошибки И-регулятора
    float DerrorDt = 0.0; //начальное значение ошибки Д-регулятора

Помимо этого, в расчетах всегда нужно учитывать граничные условия регулятора. Пример строчек кода, в которых это учитывается, представлен ниже:

If (PD_OUT > pid_border){
            PD_OUT = pid_border; //защита от ошибок регулятора 
        }
        
        If (PD_OUT < -pid_border){        
            PD_OUT = -pid_border;    
        }

Ошибки вычисляются следующим образом:

    previous_error = NormAngleDifference(phi_0 - phi_current);
        error = NormAngleDifference(phi_0 - phi_current);
        
        DerrorDt = (error - previous_error) / dt;
        
        intgral_error += error * dt;

tip

Также следует учесть, что при работе с ориентацией ОрбиКрафт 3D по магнитометру вам необходимо выполнить несколько дополнительных шагов:

1. Откалибровать магнитометр (не забудьте, что при калибровке магнитометра необходимо вращать конструктор вручную или через задание ненулевой скорости маховика);
2. Откалибровать датчик угловой скорости (ДУС).

Если после калибровки, при выполнении алгоритма стабилизации-ориентации ДУС продолжает изменять свои значения, значит конструктор не стабилизировался.

Подведём итог: пропорциональный компонент отслеживает настоящее, интегральный компонент анализирует прошлое, а дифференциальный компонент прогнозирует будущее. Суммарно – все компоненты создают нужный пользователю сигнал.

Рисунок 2. ПИД-регулятор