Lesson 11. The Doppler Effect
Theory
Doppler effect — a change in the frequency of the signal due to the movement of the signal source relative to the receiver. The effect is named after the Austrian physicist Christian Doppler.
The Doppler effect is easy to observe in practice when a car passes by the observer with the siren on. Suppose the siren gives out a certain tone, and it does not change. When the car is not moving relative to the observer, then he hears exactly the tone that the siren emits. But if the car approaches the observer, the frequency of the sound waves will increase, and the observer will hear a higher tone than the siren actually emits. At the moment when the car passes by the observer, he will hear the very tone that the siren actually emits. And when the car passes on and is already moving away, rather than approaching, the observer will hear a lower tone, due to the lower frequency of sound waves.

Picture 1. Observation of The Doppler Effect
Mathematical description of the phenomenon
If the wave source is moving relative to the medium, then the distance between the wave crests (wavelength λ) depends on the speed and direction of movement. If the source moves towards the receiver, that is, it catches up with the wave it emits, then the wavelength decreases, if it moves away, the wavelength increases:
where ω0 is the angular frequency at which the source emits waves, c is the velocity of wave propagation in the medium, v is the velocity of the wave source relative to the medium (positive if the source approaches the receiver and negative if it is removed).
The frequency recorded by the stationary receiver
Similarly, if the receiver is moving towards the waves, it registers their crests more often and vice versa. For a stationary source and a moving receiver
where u is the velocity of the receiver relative to the medium (positive if it is moving towards the source).
Substituting instead of ω0 in formula (2) the value of the frequency ω from formula (1), we obtain the formula for the general case:
Observation of the Doppler effect
We will observe the Doppler effect using the example of receiving a telegraphic code from satellites. Get ready for work and set up the necessary software as described in Lesson 09.
Wait for a "good" satellite flight at an altitude of at least 30° above the horizon.
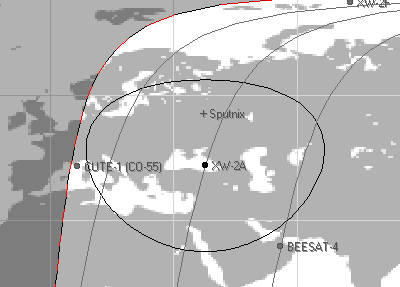
Picture 2. Example of a satellite flyby
Picture 3. Satellite overflight data
Put the sound on the headphones, and you will hear a change in the tone of the signal of a moving satellite.
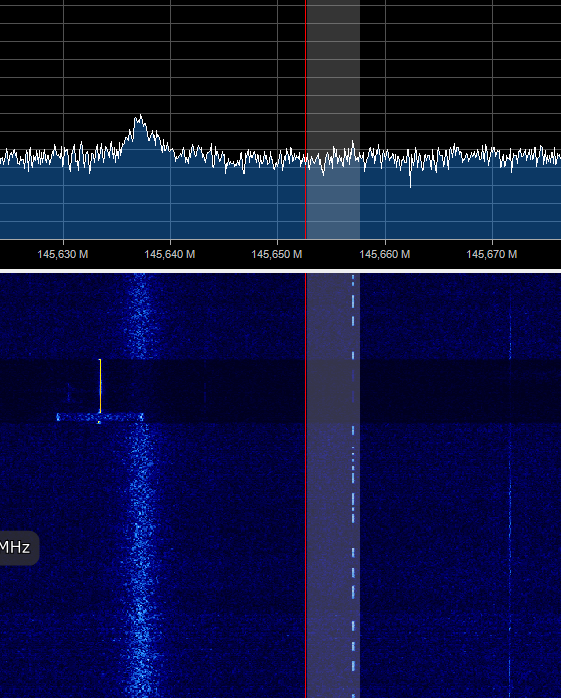
Picture 4. Satellite signal
Turn on all the items in the Zoom FFT section.
Picture 5. Zoom FFT menu
The Audio Spectrum graph clearly shows how the frequency of the passing satellite changes.
Picture 6. Audio Spectrum Graphics